Will man die Erde zerstören, hat man – das zu tun – viele Möglichkeiten. Zumindest, wenn es nur um die Auslöschung der Menschheit geht. Atomkrieg, Klimakrise oder Artensterben: Wir haben im Lauf der Zeit leider jede Menge Möglichkeiten gefunden, uns selbst zu vernichten. Aber dem Planeten ist das alles relativ egal.

Um die Erde tatsächlich richtig zu zerstören, muss man sich schon etwas mehr anstrengen. Eine Kollision mit einem großen Asteroiden könnte den Planeten beispielsweise unbewohnbar machen und die Erdkruste aufschmelzen, aber auch das würde die Erde nicht zerstören. Will man sie komplett pulverisieren, so dass nichts mehr übrig bleibt, muss man sich mit folgender Formel beschäftigen –

Diese Gleichung beschreibt die gravitative Bindungsenergie:

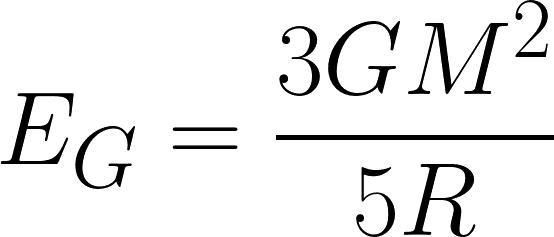
Diese Formel entspricht der Energie, die nötig ist, wenn man die durch Gravitationskraft zusammengehaltenen Bestandteile eines Körpers unendlich weit voneinander entfernen will, sie stellt den Spezialfall für eine homogene Kugel dar. Die Erde ist zwar keine Kugel und auch nicht homogen, aber die Gleichung reicht aus, um zumindest die richtige Größenordnung ihrer Bindungsenergie zu berechnen. Tut man das, erhält man ein Ergebnis von zirka 200 Quintillionen Joule. Das entspricht in etwa der Energie, die man erhält, wenn man die Masse des kompletten Asteroiden Eros (der immerhin einen mittleren Durchmesser von fast 17 Kilometern hat) direkt in Energie umwandeln könnte. Andererseits aber entspricht es nur einem Sechzigstel der Energie, die die Sonne in einem Jahr produziert.

Wenn man nicht gerade an der kompletten Zerstörung eines Planeten interessiert ist, dann ist die gravitative Bindungsenergie aus einem anderen Blickwinkel viel interessanter. Denn sie entspricht nicht nur der benötigten Energie, um den Zusammenhalt durch Gravitation aufzulösen. Die gleiche Energiemenge wird auch frei, wenn sich beispielsweise ein Stern bildet. Fängt eine der großen Gaswolken im interstellaren Raum durch äußere Einflüsse an zu kollabieren, wird sie immer kompakter. Sie fällt in sich zusammen, die Materie kommt sich immer näher und wird immer stärker aneinander gebunden. Durch den Kollaps wird die Menge an Energie frei, die durch die Formel für die Bindungsenergie gegeben ist.

Hinweise auf die Dunkle Materie

Diese Energie sorgt dafür, dass sich die Gaswolke, aus der später ein Stern entsteht, immer weiter aufheizt. Früher, bevor man wusste, wie alt die Sterne sind (und die Kernfusion noch nicht verstanden hatte), dachte man sogar, dass die gesamte Energie der Sonne aus ihrem ursprünglichen Kollaps stammt. Das hat sich zwar als falsch herausgestellt, aber man darf diese Energie trotzdem nicht vernachlässigen. Jupiter strahlt beispielsweise mehr Energie ins All ab, als er von der Sonne aufnimmt. Ein Teil dieser zusätzlichen Energie stammt von der langsamen Kontraktion des Gasplaneten, der unter seiner eigenen Anziehungskraft ein paar Zentimeter pro Jahr schrumpft.

Zu wissen, wie viel Energie nötig ist, um etwas zu binden, ist in der Astronomie generell wichtig. In den 1930er Jahren berechnete Fritz Zwicky, wie schnell sich Galaxien in einem Galaxienhaufen höchstens bewegen können, um sich nicht aus ihrer wechselseitigen gravitativen Bindung zu lösen. Das Ergebnis war deutlich geringer als die tatsächlich beobachtete Bewegung. Die gravitative Bindung musste also größer sein als erwartet. Zwicky folgerte daraus, dass eine »Dunkle Materie« die zusätzliche Gravitationskraft ausübt, die nötig ist, um den Galaxienhaufen zusammenzuhalten.