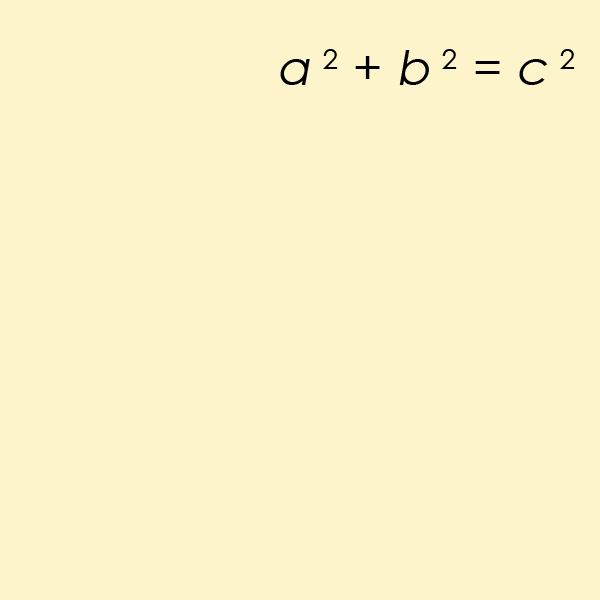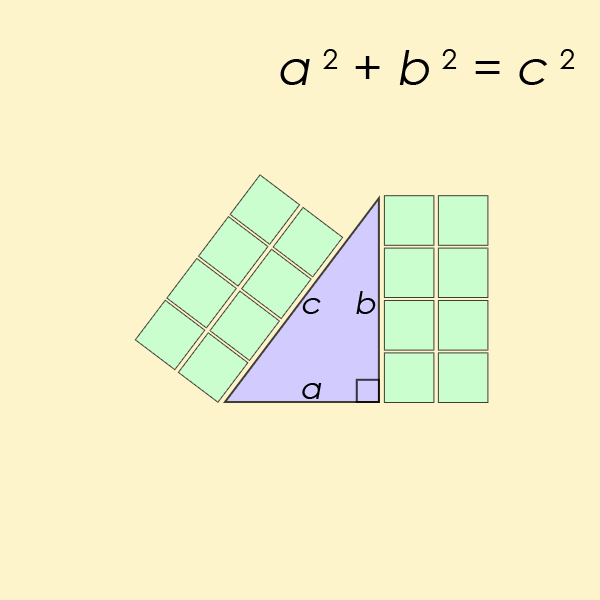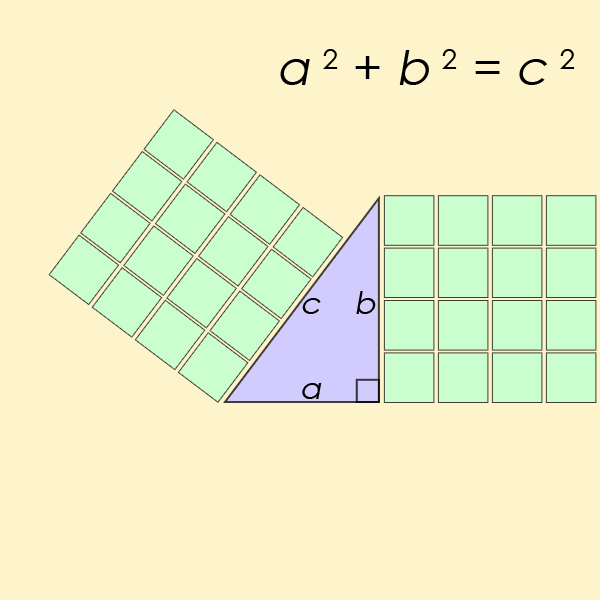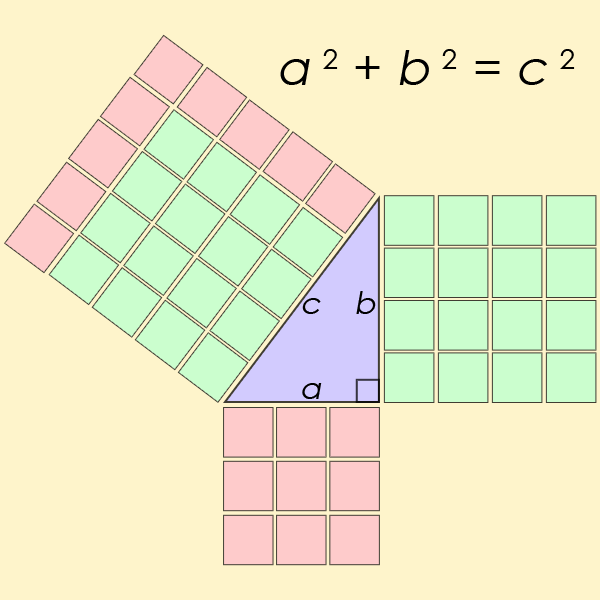Denn bei genauerem Hinsehen sticht in einer Szene ein besonderes Detail heraus: Homer steht – ganz im Stil eines nerdigen Professors – nachdenklich mit Brille an einer vollgekritzelten Tafel. Neben den obligatorischen Donuts, die nicht nur Homers Leibspeise sind, sondern gerade im Bereich der Topologie eine große Rolle spielen, findet sich eine harmlos anmutende Gleichung: 3987¹² + 4365¹² = 4472¹². Tippt man sie in einen Taschenrechner ein, erweist sie sich offenbar als richtig. Das Erstaunliche: Sie widerspricht einem der etabliertesten Theoreme der Mathematik, dem großen Satz von Fermat.

Der große Satz von Fermat: Ein jahrhundertealtes mathematisches Rätsel

Dieser stammt aus dem 17. Jahrhundert und sieht auf den ersten Blick recht einfach aus: Er besagt, dass die Gleichung xⁿ + yⁿ = zⁿ keine ganzzahligen, positiven Lösungen x, y und z hat, wenn n größer ist als zwei. Wählt man n = 1, dann ist die Gleichung immer erfüllt: Egal, wie man die Werte für x und y wählt, z wird stets ein positives, ganzzahliges Ergebnis sein, zum Beispiel: 3 + 6 = 9. Selbst Homer, der in der Serie häufig als dümmlich dargestellt wird, traut man diese Einsicht zu.

Für n = 2 wird es schon etwas kniffliger, denn die Gleichung wird quadratisch: x² + y² = z². Wenn x und y ganzzahlige Werte haben, muss das nicht notwendigerweise für z gelten, etwa ergibt für x = 1 und y = 2 die Formel 1² + 2² = 5 – und 5 ist keine Quadratzahl. Das heißt, es gibt zwar eine Lösung für z (die Wurzel aus 5), die ist jedoch nicht ganzzahlig. Dennoch findet man Ausnahmen, für welche die quadratische Gleichung doch eine passende Lösung hat, zum Beispiel: 4² + 3² = 25 = 5².