Ein paar Zahlen austauschen, um ein bisschen weniger Steuern zahlen zu müssen: Wer soll das schon merken? Das Finanzamt vermutlich – dank Mathematik.
Mathematik nämlich verwendet nicht nur Zahlen, sondern beschreibt und analysiert sie auch. Dabei ist unter anderem der Unterschied zwischen Ziffer und Zahl von Bedeutung. Im gebräuchlichen Dezimalsystem verwenden wir die zehn Ziffern 0, 1, 2, 3, 4, 5, 6, 7, 8 und 9, um daraus unendlich viele Zahlen aufzubauen. Nun möchte man meinen dürfen, dass alle Ziffern gleich häufig verwendet werden, wenn man ausreichend viele Zahlen betrachtet. Tatsächlich ist das aber sehr oft nicht der Fall, wie das benfordsche Gesetz beschreibt:
Mit p(d) wird die Wahrscheinlichkeit beschrieben, dass die Ziffer d in einer Zahl (im Dezimalsystem) an erster Stelle auftritt. Demnach findet man die 1 am Anfang einer Zahl in 30,1 Prozent der Fälle; die 9 dagegen nur in 4,6 Prozent.
Ein paar Zahlen austauschen, um ein bisschen weniger Steuern zahlen zu müssen: Wer soll das schon merken? Das Finanzamt vermutlich – dank Mathematik.
Mathematik verwendet nicht nur Zahlen, sondern beschreibt und analysiert sie auch. Dabei ist unter anderem der Unterschied zwischen Ziffer und Zahl von Bedeutung. Im gebräuchlichen Dezimalsystem verwenden wir die zehn Ziffern 0, 1, 2, 3, 4, 5, 6, 7, 8 und 9, um daraus unendlich viele Zahlen aufzubauen. Man könnte meinen, dass alle Ziffern gleich häufig verwendet werden, wenn man ausreichend viele Zahlen betrachtet. Tatsächlich ist das aber sehr oft nicht der Fall, wie das benfordsche Gesetz beschreibt:
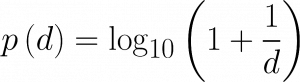
Mit p(d) wird die Wahrscheinlichkeit beschrieben, dass die Ziffer d in einer Zahl (im Dezimalsystem) an erster Stelle auftritt.
Demnach findet man die 1 am Anfang einer Zahl in 30,1 Prozent der Fälle; die 9 dagegen nur in 4,6 Prozent.
Intuitiv ist das leicht zu verstehen
Bei den Zahlen von 0 bis 9 ist jede Ziffer genau einmal aufgetreten. Zwischen 10 und 19 finden wir jede Ziffer noch einmal; nun aber steht überall die 1 am Anfang, und es dauert bis zur Zahl 99, bevor wieder alles ausgeglichen ist. Dann aber finden wir von 100 bis 199 wieder jedes Mal eine 1 am Anfang. Wir setzen Zahlen aus Ziffern zusammen, und da die 1 die kleinste Ziffer ist (führende Nullen schreiben wir ja nicht auf), taucht sie auch am häufigsten auf.
Der durch das benfordsche Gesetz beschriebene Zusammenhang gilt nicht für beliebige Zahlenmengen. Es müssen ausreichend viele Zahlen sein, die auch einen ausreichend großen Bereich abdecken. Und es müssen reale, empirische Datensätze sein, also keine Zahlen, die irgendwie manipuliert worden sind. Wissenschaftler von der Universität Wien haben zum Beispiel untersucht, ob die Preise von Produkten unmittelbar nach der Einführung des Euro im Jahr 2002 dem benfordschen Gesetz folgten – was der Fall war.
Aber schon bald danach zeigten sich Abweichungen, als die Händler die durch den Währungswechsel »krummen« Europreise auf die üblichen Werte anpassten, die knapp unter einer runden Summe lagen (zum Beispiel 1,99 Euro).
Entdeckt hat diesen Zusammenhang das erste Mal der Astronom Simon Newcomb im 19. Jahrhundert. Damals konnte man Logarithmen noch nicht mit dem Taschenrechner berechnen, sondern musste sie in dicken Büchern nachschlagen. Newcomb fiel auf, dass die Seiten, bei denen es um Zahlen mit einer 1 am Anfang ging, sehr viel abgenutzter waren als die anderen, und schloss daraus, dass solche Zahlen häufiger auftreten und deswegen auch öfter nachgeschlagen werden.
Der Physiker Frank Benford entdeckte das Gesetz im Jahr 1938 noch einmal, und nach ihm wurde es dann auch benannt. Heute wird es eingesetzt, um manipulierte Daten aufzuspüren. Wer etwa in einer Steuererklärung einfach irgendwelche Zahlen erfindet, wird dabei höchstwahrscheinlich einen Datensatz produzieren, der vom benfordschen Gesetz abweicht. Das Gleiche gilt für die Fälschung von Forschungsdaten oder die Manipulation von Wahlergebnissen. Der Astronom Boudewijn F. Roukema will dadurch beispielsweise Anomalien bei den Präsidentschaftswahlen im Iran des Jahres 2009 entdeckt haben (eine Behauptung, die aber von anderen Mathematikern bezweifelt wird).
Das benfordsche Gesetz gilt übrigens nicht nur im Dezimalsystem, sondern überall, wo Ziffern zu Zahlen zusammengesetzt werden. Dem strengen Blick der Mathematik kann man nicht entkommen – gleich wie unerfreulich die Steuererklärung ausfallen mag.
